量子テレポーテーションは、一般の方から見てやはり不思議な現象だろう。
この世の中の全てのモノの本性である、量子情報。そしてその集まりとしての量子状態|ψ〉（または波動関数ψ(x)）を、ランダムに吐き出された測定結果を遠隔地に伝えるだけで転送することが可能だ。
以前書いたブログ「量子テレポーテーションは、本当はテレポーテーションではないのか。 」でも、その概要は触れた。
そこでも説明したように、送り手のアリスとっては、量子情報が瞬間的に移動したように見える。
（ただその量子情報を受け手のボブが使えるようになるには、光速度以下で届く測定結果を知る必要があるが。だから因果律は破れない。）
ボブにとっても、テレポーテーションが終わってから自分のスピンの過去の状態を推定すると、測定結果が届く前から、未知の状態|ψ〉に依存したある純粋状態だったように見える。
更にアリスが測定する前からその純粋状態だったようにすら思えるのだ。
つまり量子情報は超光速で先回りして、ボブのスピンに入っていたように考えることもできる。
しかし量子状態を情報の束に過ぎないとみなすコペンハーゲン解釈では、全く問題が生じないことも先のブログ記事で説明した。
今回、説明しようとすることは、その量子テレポーテーションという手品のタネである。
このマジックの中でアリスからボブの間の空間を伝わるのは、|ψ〉に依存しない確率分布をする２ビットの古典情報（測定結果）だけだ。
それなのに、いつのまにかボブのスピンは|ψ〉の情報を持っている。
その仕掛けの舞台裏を、新たな登場人物のクリスからの視点で見てみよう。
再び２準位スピン系の量子テレポーテーションを例にして考える。
アリスは謎の人物から渡された未知の量子状態|ψ〉にあるスピン１を持っている。
その状態はスピンの回転軸が上を向いている状態|+〉と、下を向いている状態|-〉の量子的な重ね合わせにはなっているはずだ。ただアリスやボブは、その重ね合わせの複素係数を知らない。
その未知の状態|ψ〉をアリスはボブに壊すことなく転送しなくてはいけない。
単にスピン１を観測して、得られた|ψ〉の情報をボブに知らせればいいじゃないかと思う人もいるかもしれない。
しかし古典力学と違って量子力学では、１つしかないスピンを測っても|ψ〉はほとんど確定しないし、更に悪いことにその観測によって状態|ψ〉が壊れてしまう。
そのような難しい要求であるが、共有していた最大量子もつれ状態にあるスピン２とスピン３を使って、|ψ〉の中身を知ることもなく、アリスとボブはこの転送をやってのける。
もちろんスピン２と３のこの状態は、|ψ〉に依存していない。
２つのスピンの最大量子もつれ状態には連続無限個の種類があるけれど、その中から互いに直交する下記の４つのベル状態を考える。
そしてアリスがもつスピン２とボブがもつスピン３は、最初はこのＩという名前のついたベル状態だったとしよう。するとテレポーテーション前の最初の状況は図３のようになっている。
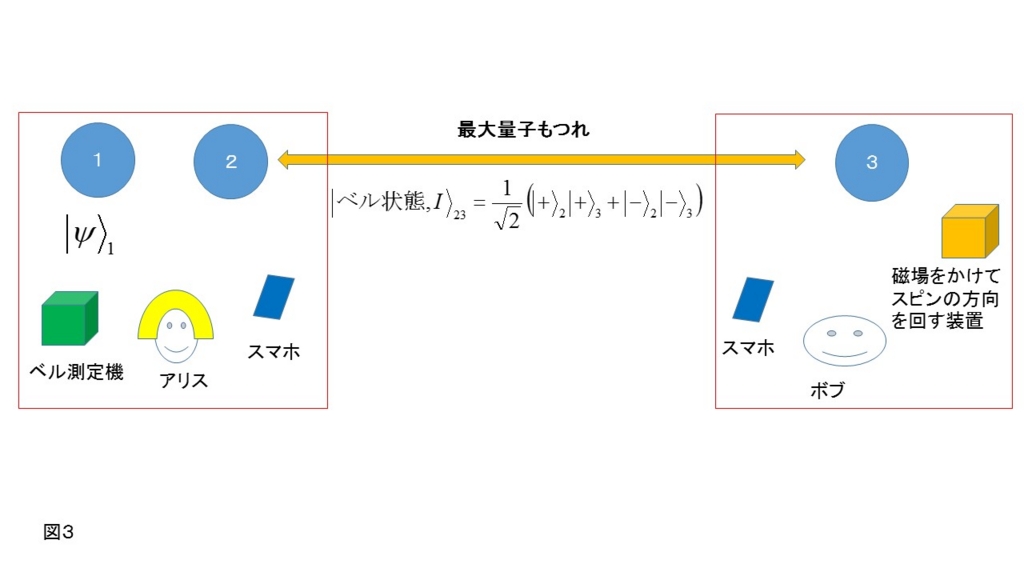（ここで各ケットべクトル|⋅〉に添えられている数字は、その状態にあるスピンを指定している。）
アリスの領域には未知状態|ψ〉のスピン１と、ボブのスピンともつれているスピン２。そして、その２つを観測する測定機と、その結果をボブにつたえるスマホが置かれている。
ボブの領域もスマホがあり、スピン３とそれに磁場をかけられる装置もある。
さてテレポーテーションの構造はすでにこの段階で見えている。
図４のように、この３つのスピンの合成系の初期状態は、４つの異なる状態の量子的な重ね合わせだからだ。
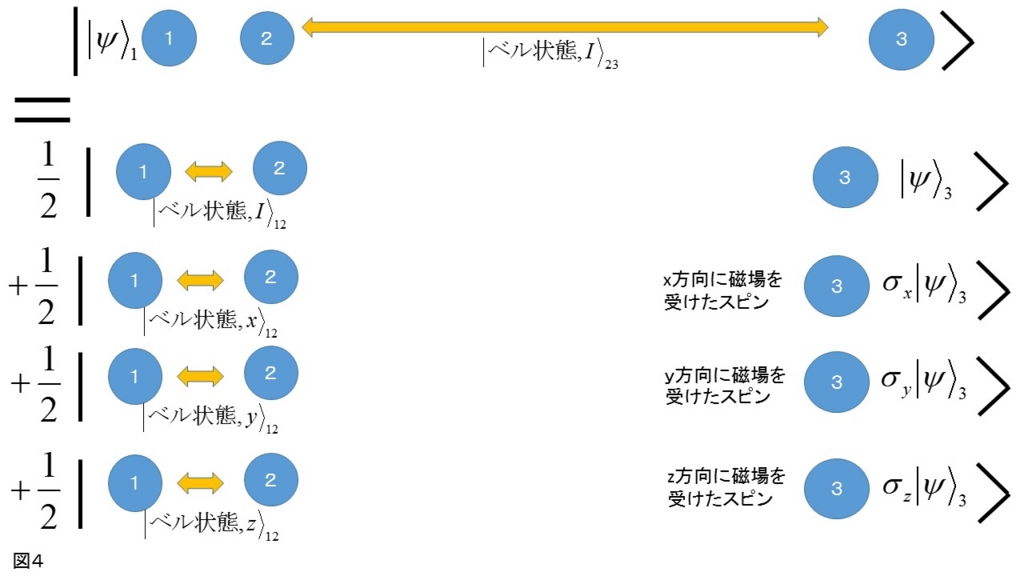それぞれの状態で、特にアリスのもっているスピン１とスピン２は図２の最大量子もつれ状態（ベル状態）のどれかになっている。一方ボブのスピン３は、各状態において既に|ψ〉依存性をもっているように見える。数式で書けば、下のようになっている。
しかしこれをみて、最初からスピン３は|ψ〉を知っていたと思ってはいけない。
アリスの領域の２つのスピンの自由度を無視（数学的には縮約）して得られるスピン３の状態は、単位行列に比例する最大エントロピー状態であり、|ψ〉の依存性は実際にはない。
だからこの段階でボブがいくらスピン３を測っても決して|ψ〉の情報を知ることはできない。
この"テレポーテーションマジック"では、アリスがまずスピン１とスピン２を測って、図２の４つの状態のうち、どれになっているかを測定機を使って確かめる。
測定後、スピン１とスピン２はどの場合でも、|ψ〉に依存しない最大量子もつれ状態になっている。また連続無限個の種類がある純粋状態の中から任意に１つの|ψ〉を選んでも、出て来る結果の値の確率は常にどれもp=1/4であり、全くランダムな確率分布をしている。アリスにとっては、もう自分の領域のどこにも|ψ〉に関する情報が見つからない。そして彼女にとっては、知識の増加としての波動関数の収縮により、その量子情報は既にボブのスピン３に飛んでいる。
普通の場合、情報は何かの移動する物体に刻まれて、アリスとボブの間の空間のある経路を通って伝わるはずだ。
ところが実際にはどこにも|ψ〉の情報が通過した形跡がないから、量子テレポーテーションは確かにテレポーテーションに見えるわけだ。
図７のように、その後アリスはその２ビットの古典情報をスマホを通じてボブに伝える。
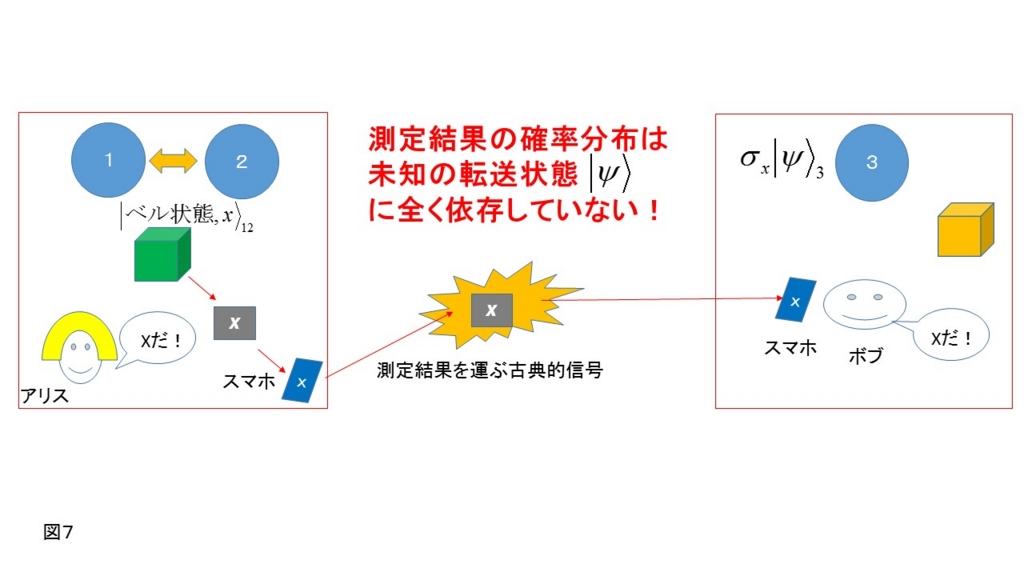そしてボブはアリスの結果に応じて向きを選択して磁場をスピン３にかける。その結果図８のようにスピン３の状態は１００％の確率で、最初の未知状態|ψ〉になる。
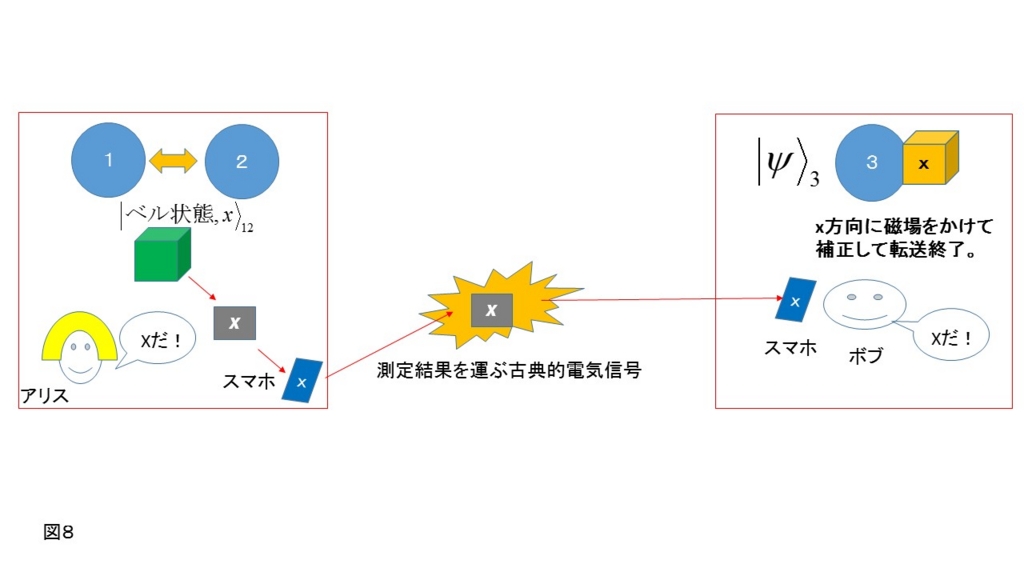（図７、８では、出力された結果がｘの場合で書かれている。）
アリスの測定直後からアリスの領域のどこにも|ψ〉が見つからないのは、やはり不思議な手品のような現象だ。
実は、舞台裏のクリスには、そのタネがよく見えている。
量子力学はマクロな系でも成り立つと考えられるので、クリスにとっては、スピンだけでなく測定機やスマホ、そしてアリスやボブまでも、量子的な系になっている。
量子テレポーテーションの各ステップも、その量子系で起きるユニタリーな量子過程に過ぎない。
そしてアリスの測定終了直後、クリスにとって、アリスの領域にあるもの全ては、図９にある４つの異なる歴史をもつマクロな量子状態の重ね合わせになっている。
その全体系の状態を数式で表すと、下のように書ける。
この状態で、ボブのスピン３の自由度を無視（縮約）して得られる、アリス領域の量子系の縮約状態は下記のものだ。
このアリス領域の状態の重要な特徴は、未知状態|ψ〉の依存性が全て干渉項のみに現れていて、対角成分のどこにもでてこない点にある。
アリスの測定後にその領域から消えたように見えていた|ψ〉の情報は、マジックの舞台裏のクリスから見ると、マクロ系の量子もつれの中へ巧妙に隠されていたのである。
この他の場合でも量子もつれを使うと、各部分系には情報をまったく持たせないまま、情報を壊すことなく完全に隠すことは可能だ。ブログ記事「量子エンタングルメントと時間の矢 」の中でも、そのような他の例が紹介されている。
図１１の数式の干渉項の最後の部分に出ている|ψ〉に対する２点相関関数は、どれも３つのパウリのスピン行列の|ψ〉での期待値に一致することも、スピン行列の性質からすぐわかる。
そしてこの３つの期待値がわかれば、純粋状態に対する下記のブロッホ表示を使って、|ψ〉は完全に定まる。
だから図１１のアリス領域の量子系の状態を何回も用意して調べれば、その３つの期待値は測定され、そして|ψ〉が再現されてしまう。またこの時点でボブのスピンの縮約状態にはやはり|ψ〉の依存性が全くないことも、もちろん確認できる。
このことは、測定直後にクリスから見れば、|ψ〉の情報全てはまだアリスの領域に隠されて留まっていたことを意味する。つまりスピン３には全く届いていない。
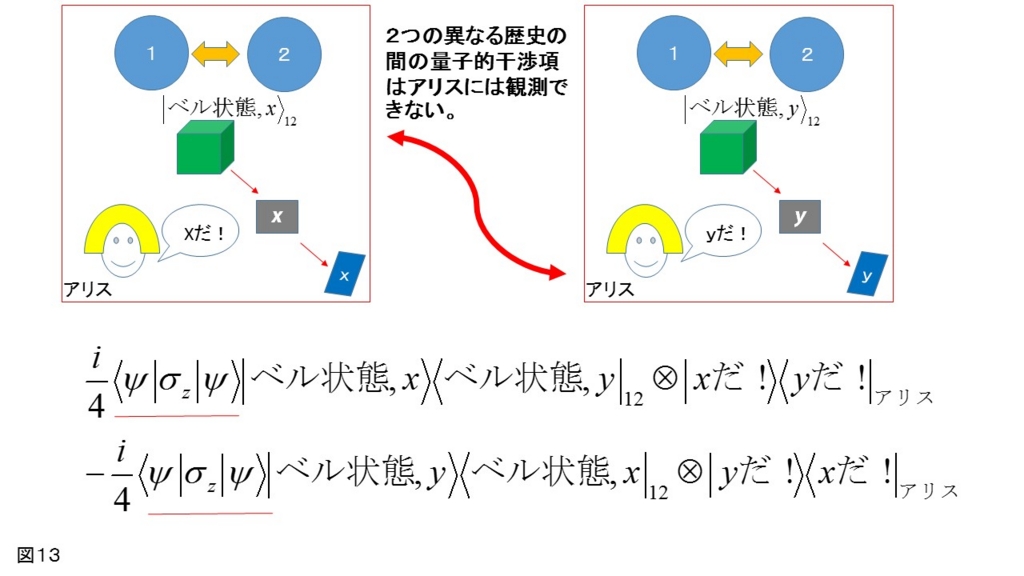
図１３に書かれている干渉項の１つの成分部分のように、干渉項の中に|ψ〉を隠すというトリックだったのだ。
アリス自身が参加している異なる歴史どうしの干渉であるため、決してアリスはこの干渉項を観測することができないという、量子力学の原理に則った究極のトリックである。(アリスは、４つの歴史のうちの１つだけしか、意識できないため。)
クリスからみれば、アリスからの情報をスマホで受け取り、その結果に応じてボブが行う磁場をかける図１４の操作も、もちろんユニタリー過程だ。
舞台裏からこの過程を見れば、アリスのところから送られた信号にもその干渉項部分に|ψ〉の情報が隠されており、因果律に則った光速度以下のスピードでスピン３にそれは届けられ、こっそりと受け渡されていたのだ。
クリスにとっては、図１４の操作はスピン３への情報書き込みだけでなく、スピン３と他の系の間にあった量子もつれを解消する「dis-entangler」の役目もしている。
これがクリスの視点からみた、テレポーテーションマジックのタネの全貌である。
ただ強調しておくと、普通の手品とは違い、クリスの視点が正しくて、アリスやボブの視点での描像が間違いだとか、不正確ということではない。
アリスがみる量子状態、ボブがみる量子状態、そしてクリスがみる量子状態は、観測者のもつ系の知識量の差によって、一般には全て違う。
量子力学は観測者毎に定式化されており、どの視点での描像も互いに矛盾を起こさない。
クリスにとっての量子力学では、まったく異なる歴史の間に生じる「干渉項」に隠されて量子情報は空間を伝達し、アリスにとっての量子力学では、確かにアリスが測定した瞬間に、量子情報は既にボブのスピンに飛んでいる。
アリスの見方でも、クリスの見方でも、量子テレポーテーションの描像は日常生活とかけ離れているものだが、それぞれ間違いではない。
これが、量子力学自体の深さを示しているところなのだ。
通常粒子の復習から入ろう。
だから平坦な時空上での
するとよく知られているように、エネルギーと運動量の間には上式の関係が成り立つ。
ここで世界線のアフィンパラメータはλと書いてあり、上の関係を満たすものとする。
ここでのポイントは、μを正にとっている限り、
すると
実はこの保存則こそが体積
これはJの第ゼロ成分の体積
ここでLは
すると今度は、t=±Tに対応する線
同様のことをエネルギー運動量
このチルダ付きの時間
これを用いると以下のように、上で定義されたチルダ付き時間
また通常物質と
冷却原子にQCDなどの非可換
綿密に練られた構成と繰り返された練習を背景にして聴衆を見事に引き込み、一番多くの関心を呼んだ。