
教科書の第3章に関連したコメントがあったので、補足をします。この教科書は、既存の実験結果、もしくは未知の対象系に対して実験で将来検証可能な形の仮説を与え、それを用いて沢山存在する理論の可能性の中から、量子力学という1つの定式化を作っていくというスタイルです。第3章では、第2章の2準位系の量子力学の定式化を多準位系に拡張することが書いてあります。
そのコメントとは、「多準位系で純粋状態が複素列ベクトルで表せることや、そのボルン則を示すことなどを演繹的に示すのは、強引な前提を導入しない限り難しいのではないか」「なぜ多準位系で複素ベクトル空間を考える必要があるのかを論理的に説明することは困難だろう」という趣旨の内容でした。指摘されたこのコメント自体は、後で説明をするように、実はこの教科書の論理の流れには当たらないのですが、教科書には厳しいページ数制限があったために、十分な説明が足りていなかったようです。また2準位系と「みなす」ことや3準位系と「みなす」という意味についての部分が抜けていましたので、それらの補足説明を以下でしたいと思います。
まず再度強調したいことは、量子力学は確率論に基づいた情報理論の一種であり、そのような理論は量子力学以外にも無数にある点です。その多準位系の理論でも、既知の2準位系の定式化を様々に拡張する可能性もあり、それぞれについて理論を作ることが可能です。ただその多くは既に実験と合わないことも知られています。そこでどのような実験事実、または実験可能な仮定を基礎とするかが構成の鍵になります。
まず第2章の2準位スピン系の話から参りましょう。教科書では基準測定であるスピンz成分のシュテルン=ゲルラッハ(SG)実験を使って、量子力学の体系を作っています。なぜ2準位系と「みなす」かと言うと、装置から出てくるのが区別された2つの状態であるからでした。
ただ現実の物理系の実験は全てのエネルギースケールで行っているわけでもありません。例えば現在行われている高エネルギーの素粒子実験では、電子のスピンは確かに2つの状態のみを持つことと整合した結果しか得られておりません。しかし可能性として(これは深い理由があるものではなく、単なる論理的な可能性ですが)、より高いエネルギーで実験をすると実は電子スピンにはもう1つの状態がある3準位系になっていても良いわけです。もちろんそのようなことを示唆する実験も理論も現在ありませんが。
仮にそういうシナリオを考えたときに量子力学でのそのスピンの扱いはどうするかという問題があります。これに対しては2つの可能性があります。
まず第1の可能性として、SG実験で出てくる出力ビームが3本に分岐する場合があります。このときは2準位系の扱いのままで良いわけがありません。きちんと3準位系として理論を組み立て直す必要があります。
第2の可能性は非常に変わった状況ですが、基準測定としてのSG装置から出てくるビーム自体は常に2本のままという場合です。SG実験以外の測定法では新しい高エネルギー状態の寄与が観測できるのですが、元々使っていた低エネルギー領域での物理量のみを測るSG実験では、その高エネルギー状態の寄与が全く見つけられない場合です。この場合は、第2章2.1.2節のスピン期待値のベクトル性さえ満たせば、それ以降の教科書の議論はそのままその3準位系に使えるのです。つまり3準位系の低エネルギー部分に対しては、2準位系量子力学の枠組みでそのまま記述できます。そしてその量子状態を密度行列や状態ベクトルで表現することが可能なのです。高いエネルギー領域では異なる理論でも、同じ2準位系量子力学で記述できるということになります。実はこの量子力学形式の汎用性の高さが現れるのは、高エネルギー領域では異なる理論に限りません。例えば1つの2準位スピン系ならば教科書付録Gにある隠れた変数の理論でもSG実験の結果を再現しますが、この局所実在論すらも、複素ベクトルや行列を用いた2準位量子力学で書き表すことは可能なのです。様々な理論を飲み込めるこの量子力学という言語の枠組みの懐の深さは、後で見るように2準位系に限らず多準位系でも同じです。
このように、まず2準位スピン系の2準位量子力学が作られました。このことから教科書で触れているように、一般の2準位系でも同じく、その2次元状態空間に作用する任意の2次元ユニタリー行列には、対応する物理操作があるわけです。「あるわけです」とさらっと書きましたが、ここに重要な(でも極めて自然であり、従来はわざわざコメントもされない)理論の仮説がまず入っていることに注意をしてください。
一般に物理学の基礎的な理論を作るとき、個々の物理系ごとに異なる法則や定式化を作ることは行いません。全ての系に共通する普遍的な法則を記述するために、どんな物理系にも適用可能な一貫した理論体系を構築する必要があります。教科書第2章で扱われる2準位系は主に2準位スピン系でした。その特別な系で成り立つ方向量子化やスピン期待値のベクトル性の実験結果に基づいて、ボルン則や量子状態の重ね合わせの存在を示したわけです。その特定のスピン系で作られた理論が他の任意の2準位系(それは未知の物理系かもしれませんが)でも成り立つような理論であると仮定する姿勢は、普遍性という物理学の目的を考えると、極めて自然で正常な姿勢とも言えます。それで未知の系も含めた任意の2準位系に対しても、第2章の定式化によって「2準位系量子力学」という理論自体を定義しました。後は未知の2準系が見つかるたびに、この理論が実験と整合するかを確かめ続ければよいのです。
さてまだ見つかっていない物体に対しても適用をしたい。このような理論の普遍性を、多準位系の量子力学という理論に課すのはとても自然なことです。ただし今はもう2準位系の量子力学を作ってしまったので、それと整合するように多準位系量子力学を構成するべきです。教科書の第3章でも、そのような精神に則って理論を構築してあります。
以下では先のコメントにある内容が第3章の論理展開には当てはまらないことを理解するために、具体的に3準位系を例として用いて、補足をしたいと思います。まず2準位系と同様に、実験設定から第3章は始まっています。2準位スピン系のSG実験と同じ役目をする基準測定の話です。

3準位系なので、図1のように左側から量子系を基準測定の装置に入れると、右側には3つの異なる状態が出力されます。それらを上から状態1、状態2、状態3と呼ぶことにします。ある状態にある3準位系を測定機に入力したとき、図2のように状態1にその系が現れたとしましょう。

この状態1は純粋状態の1つであると定義をしたくなる理由は、出てきた系にもう一度同じ基準測定をすれば分かります。これは例えばスピン量子数が1である3準位スピン系を、SG装置に通す実験を思い出せば、より分かりやすいでしょう。図3のように、必ずその系は再び状態1に確率100%で現れます。これは2準位系のSG実験の拡張であり、たとえ未知の3準位系でも、必ずそのような測定機を作ることが可能であるという仮定を、理論として行います。これが量子力学という理論なのです。ここで注意して頂きたいのは、この仮定自体は将来実験で検証可能ですが、そのような実験が行われて理論の予言通りになったときだけ、量子力学という理論はその系に適用可能という点です。もし成り立たなければ、その時には量子力学を捨てる必要が出てきます。網羅的な実験を行って、ある特定の物体には基準測定が存在しないという結果を得た人は、間違いなくノーベル賞を受賞することでしょう。(その未来にノーベル賞自体があればですが。)

2回目の基準測定の結果が変わらないこの性質のことを、反復可能性と呼ぶこともあります。量子力学がその系に適用可能なためには、この反復可能性が状態2や状態3でも同様に成り立つ必要があります。図4のように状態2に用意された系を再び測定しても、図5のように状態2として観測されます。状態3でも同様で、図6図7のようになります。




この基準測定で同定される純粋状態に物理操作(これは未実験の高エネルギー領域での測定は含まない条件での任意の測定や確率混合も含みます)を行うことで、様々な状態の準備が行われます。そしてこの状態の集合が、3準位系量子力学での状態空間として定義されるのです。
このように状態準備でも物理操作が重要なので、それを次に考えましょう。第2章の2準位系でも空間回転という物理操作が重要でした。多準位系でも、第3章では物理操作を一番の注目ポイントにして考えていきます。

図8のように、基準測定をする前にその系に対して物理的な操作を行ってみましょう。この各状態が出現する確率は、その物理操作に依存するようになります。なおこの物理操作が、高エネルギー領域で初めて現れる第4の状態の寄与を系に与えたとしても、装置からの出力は常に3つであり、その出現確率の和は1であることが、先に述べた通りに前提となっています。
ここで第2章の2準位スピン系での方向量子化と同じことを実験装置で確認をしておくのは重要です。つまり任意の物理操作をした後でも、装置から出てくる状態1、状態2、状態3を表す信号の装置内での位置はその操作に依存しないという点です。これは既存の3準位系の一部では実験的にも確立している事実であり、また未知の3準位系に対しては、量子力学ではそれを仮定する(または予言する)ということになります。このおかげで、左から入力された対象系ビームに対する3本の出力ビームの位置がその操作によってどのくらい移動するかなどの詳細を気にする必要はなくなり、図8のように3本の出力状態が出ているだけの情報しか描かれていない簡単な図を使って、本質的なことが議論できるのです。この辺りのことは、図を用いた操作論の量子論の数学的な教科書等ではあまり触れられていない、物理学として重要な隠れた前提だったりします。操作を表す図を組み合わせた数学的な取り扱いの裏には、このような物理的な、または実験で積み重ねられた多くの事実が前提とされています。この物理的な前提の重要性も、本当は実証科学としての量子力学において強調されるべき点だと考えられています。
図9のように、状態1に用意された系に対してある操作を行うと、状態3が出る確率は零のままで、状態1と状態2が観測できる確率がそれぞれ非零になるような状況を考えます。この「考えます」というのは、「量子力学という理論が正しいとすると、そのような物理操作が世の中に必ず存在するはずである」という意味です。ある未知の3準位系が本当に量子系であるかどうかを確認するためには、基準測定の反復可能性の実験の後に、そのような実験を一生懸命試みる必要があるのです。なおこれは理論物理学者の仕事ではなく、実験物理学者の腕の見せどころでもあります。


さてうまく実験家が図10のような測定を実現できたとしましょう。このとき図9の物理操作によって、状態1と状態2の間の「2準位系」を構成できたことになります。この「2準系」に対して教科書第2章の理論の予言を確かめる実験を行うわけです。量子力学という理論は、任意の2準位系のどれでも、全く同じ定式化で記述されると宣言をしているわけですから、それを実験で確かめられます。無事そのテストを合格して、第2章の2準位系量子力学が生き残るのならば、その部分では必ず状態ベクトルや密度行列で状態は定義可能となります。また普通の実数値で定義された任意の2準位系の物理量も、エルミート行列を使って表示することが可能になります。
図9や図10では状態1と状態2に注目をしたわけですが、ここで状態3を仲間外れにすることは不自然です。ですから同様に、例えば図11や図12のように、状態2と状態3も2準位系とすることを理論として許容することはとても健康的です。ただこれも実験家が頑張って後で確かめることになります。


同様に、状態1と状態3からも第2章の2準位系が作れるわけです。
以降では、図13のように、物理操作を可逆なものに限定してみましょう。第2章のスピン系では、それは空間回転という操作に対応し、ある角度の回転操作の逆操作は、符号を変えた同じ大きさの角度の回転操作でした。このような可逆な物理操作が多準位系でも存在すると仮定をします。これも確かめるのは実験家です。(怠け者の理論家に比べて、実験家はいつも大変なのです。)

3準位系では、第2章の意味での状態1と状態2の間の2準位ユニタリー的物理操作と、状態2と状態3の間の2準位ユニタリー的物理操作とがそれぞれ可能です。その行列と具体的な物理操作の紐づけも実験で可能であり、その紐づけ対応の全体的なリストを作ることもできるはずです。また物理操作なのですから、図14のように、その2つを対象系に対して連続して実行することも可能なはずです。

その操作の後で基準測定をしたときに、現れる各状態の確率はどのように計算されるべきなのでしょうか?状態1と状態2の間の物理操作は、第2章の2準位量子力学で図15のように2次元ユニタリ行列で既に表現されています。状態2と状態3の間の物理操作でも、図16のように同様にできます。


ここで図17のように、各2準位系としての2次元ユニタリ行列を並べてみましょう。

例えば状態1と状態2の間の2準位ユニタリな物理操作は、状態3に全く影響を与えないと仮定することは自然に思えます。同様のことが状態2と状態3の物理操作、状態1と状態3の物理操作にも言えます。この方針で拡張をして得られる理論こそが、実は3準位系の量子力学なのです。これを理論として実現させるのは簡単です。図18のように、各2準位ユニタリ行列に、影響を与えない状態に対する射影演算子を加えるだけで良いのです。赤字で強調した寄与がそれです。

この仮定も未知の3準位系に対しては実験で確かめるべきことですが、既存の3準位系では、実際にこの性質が成り立っていることも実験で検証済みであることも多いのです。また図18のユニタリ行列を組み合わせて掛け算をすれば、N=3の場合の(3.11)式のように、任意の3次元ユニタリ行列が再現できます。(3.11)式右辺の各2準位ユニタリ行列には物理操作が既に紐づけされているのですから、その物理操作を(3.11)式右辺の積の右から左に向けて順番に行えば、(3.11)式左辺の3次元ユニタリ行列に対応する物理操作が作れます。この事実を踏まえて「任意の3次元ユニタリー行列に対して物理操作が存在する」という仮定によって定義されるのが3準位系量子力学であると、図19のように教科書第3章で説明をされているのです。実際には一般のN準位系で解説をしています。N=3の場合と同様に、教科書の(3.11)式左辺のN次元ユニタリ行列に対応する物理操作は、右辺に現れる2準位ユニタリ操作の組み合わせで物理的に実験できます。したがってどのように実験をすれば良いのかについても、とても見通し良いものになっているのです。

後は第3章3.2節の話を踏まえることで、多準位系で純粋状態が複素列ベクトルで表せることや、そのボルン則を示すことなどが実際に「演繹的」に示されているわけです。
それをもう少し丁寧に解説をしておきましょう。方針は第2章の2準位スピン系の定式化です。それにはスピン期待値のベクトル性にあたる現象をきちんと押さえておく必要があります。そのためまずは普通の量子力学を先取りして、第3章の順に沿って10個の物理量の測定を行い、その期待値を評価します。そしてスピン期待値のベクトル性の拡張版の関係式の形を3準位系で押さえておきます。(何を測定すれば良いのかの目星をつけるために量子力学の先取りはしますが、その実験に基づいた量子力学の理論構築の話はトートロジーにはなりません。全ての量子力学の知識を忘れて、得られた実験データのみから一意的に量子力学の体系を再現する話になっています。)
ここでは知っている量子力学を仮定してこの関係式を先に作っておくのですが(2準位スピン系でのスピン期待値のベクトル性の関係式も、その形は実験の前に事前に計算して知っていたのと同じ)、この得られた関係式に出てくる諸量は後で全て実験で検証できるものになります。そしてこの途中計算を完全に忘れて実験だけをし、「スピン期待値のベクトル性の拡張版の関係式」が実際にデータで確かめられたと仮定して、元の3準位系量子力学の理論体系を、実験データだけから一意的に再構築できるかという問題を改めて考えるのです。
ではその関係式の形を知っておくことから始めます。(3.11)式でN=3とした関係に現れる2つの2準位ユニタリ行列は、図21のようにそれぞれがある具体的な物理操作に紐づけされています。

この2つの物理操作を連続することで定義される図22の物理操作が、先ほどの3次元ユニタリ行列に対応する物理操作であると同定されます。そして実験ではこの紐づけを使います。


つまりこの合成された物理操作を対象系に実験で作用させて、その後で基準測定を図23のようにするのです。この基準測定では各状態が現れる確率分布が定まります。それを使うことで、第3章の(3.2)式と(3.3)式を満たすように定義された2つの物理量を測定し、その期待値を図24のように計算します。この物理量は、回転操作をして傾けた方向の2準位スピン成分の3準位系への拡張になっています。これが済むと、教科書第3章3.1.1節(3.5)式から、この2つの期待値によって図25のように各状態の出現確率が得られます。


ここで第3章3.3節にありますように、この図25の実験はエルミート行列で指定される任意の物理量の測定にもなっていることに注意をしてください。

量子力学という理論の目的は、与えられた初期状態に対して任意の物理量の値の確率分布を計算することにあります。ですから図24の設定の実験をすることが不可欠です。これが2準位スピン系でのスピン期待値のベクトル性の関係式の拡張を3準位系に与えます。

3.3節から3.8節までの議論を辿ることで、図27のように各状態や物理操作は密度行列とユニタリ行列で書かれることが保証されます。それが操作後の確率分布を定める2つの物理量期待値と、操作をしないで測定した8個の物理量期待値の関係式を与えるのです。
まずトレースの性質を使って、図28中の数式のように、2つの期待値の式は変形できます。


図28の右辺に現れた行列は、図29の数式のようにSU(3)代数の元である8個のエルミート行列を使って書けることが数学で知られています。これを使うと

と2つの物理量期待値は計算されます。そのため最初の2つの物理量期待値は物理操作をしない状態で測定された8つの物理量期待値と下記のように結びついていることが示されます。

この関係式こそが、図32のように、2準位スピン系のスピン期待値のベクトル性の関係式の拡張になっているわけです。

この関係式は実験で検証できる操作論的なものになっています。この関係式が実際に実験で確定さえすれば、その実験データだけから3準位系の背景にある理論は、第2章のように状態ベクトルやエルミート行列で書かれる量子力学の形式で表せることが、自然に演繹されてくるのです。

ではここで3準位系及び多体系の量子力学の定式化のための前提をまとめておきます。

もう少し具体的に、図32中の関係式が実験で成り立つ確率論は、必ず量子力学で書けることをN準位系で見てみましょう。教科書の(3.11)式をまず思い出してください。これはN×Nユニタリ行列の数学から得られる関係式で、いつでも成り立ちます。

右辺の各2準位ユニタリ行列はそれぞれ既に具体的な物理操作と紐づけされています。そこで実験では、図34のように連続した物理操作を左辺のN次元ユニタリ行列に対応させます。

次に教科書3.1.1節で解説されている物理量と基準測定を考えます。すると(3.5)式が導かれます。

この図35の実験をすることで、図36中のスピン期待値のベクトル性を示す関係式の拡張版が成り立つことが確認されたとします。

特に図36に出ている関係式右辺に現れた係数は、図37に書かれている群論の関係式の係数と一致していることも実験で確かめられたとします。この実験結果が成り立てば、この系を記述する確率理論は行列を使った量子力学で表すことができるのをみてみましょう。

この実験の背景にある確率理論を量子力学の表記で書くには、図38中にある量子状態トモグラフィの数学的関係を用います。

この量子状態トモグラフィの関係式を使えば、図36の関係式左辺のN-1個の物理量期待値は

と計算できるわけです。そしてこの計算の最後の式において

と書いてみます。すると図35中に出てきた確率は下記のように書き表すことができます。

ここで教科書の(3.21)式を使います。これも単なる数学であり、いつでも成り立ちます。
 これを使えば、下記の関係も導けます。
これを使えば、下記の関係も導けます。

また図35中に出てきた確率は、簡単に次のようにも表せます。
 これは量子力学のボルン則そのものですね。この関係式の左辺でkの和をとれば、全確率が1であることから、密度行列のトレースはいつも1であることも示されますし、また実験で確かめられた図36の関係式を踏まえると、図37のN次元ユニタリ行列は任意にとれるので、確率の非負性から密度行列の非負性も再現できています。
これは量子力学のボルン則そのものですね。この関係式の左辺でkの和をとれば、全確率が1であることから、密度行列のトレースはいつも1であることも示されますし、また実験で確かめられた図36の関係式を踏まえると、図37のN次元ユニタリ行列は任意にとれるので、確率の非負性から密度行列の非負性も再現できています。
この教科書では、基準測定の出力として出てきた1つの純粋状態には、(3.6)式の状態ベクトルを定義として対応させます。基準測定機から出力されたk'番目の純粋状態に対して何も他の物理操作をせずに2回目の基準測定をすれば、反復可能性から測定結果は100%同じk'を出します。他のk'の値が出る確率は零です。そしてこの純粋状態に先の物理操作をした後の状態は下記のように表されます。
 ここで操作後の状態ベクトルを下記のように導入することができ、よく見る状態ベクトルに対するボルン則が得られます。ここに現れたN次元ユニタリ行列は(3.11)式から任意のユニタリ行列をとれます。従って任意の状態ベクトルがこの系の1つの状態を記述できることが分かりました。
ここで操作後の状態ベクトルを下記のように導入することができ、よく見る状態ベクトルに対するボルン則が得られます。ここに現れたN次元ユニタリ行列は(3.11)式から任意のユニタリ行列をとれます。従って任意の状態ベクトルがこの系の1つの状態を記述できることが分かりました。

これまでのことが、教科書第3章3.2節の終わりに書いてある「ただしこの前提は、飽くまでも各系において、実験で検証されるべきことである。」の詳しい内容となっています。この議論では、全て実験で検証可能な仮定ばかりを使っていますので、「強引な前提」は導入されておりません。そのような自然な仮定に基づいた拡張によって、一般のN準位系でも、複素ベクトル空間で記述可能な量子力学という体系が組みあがっているわけなのです。どんなNの値に対する未知の系であっても、量子力学は上で述べた実験可能な仮定から絞られている理論であるということは、とても興味深いですし、重要なことだと思っています。
再び強調しておきますが、今後も観測されたり、作られたりした物理系が「量子系」であるかどうかを実験で確かめ続けることは、とても大切です。量子力学は飽くまで実証科学の物理学の理論であり、実験に基づかない抽象的な数学的公理から導けるものではありません。その意識をしっかりと読者の皆さんにも持って頂ければと願っております。
最後ですが、この「補足」は、中平健治さんと松本啓史さんとの議論の中から刺激を受けて、何度も再整理をし、加筆をいたしました。彼等に感謝いたします。
追記:量子力学という理論の公理や前提を最初に述べて、その理論の帰結を示していくスタイルの教科書が主流ですが、そのデメリットもコメントしておきます。ある物理系が量子力学で記述される量子系であることを実験で確かめたい場合、公理から予言される現象をいくら実験で確認しても、どの段階からその系が本当に量子系であると断言できるかが曖昧なわけです。「これだけ沢山整合する実験結果もあるし、多分量子系であろう」という感じに終始してしまうのが、公理から出発する量子力学体系の弱点です。本教科書のスタイルには、最小限これだけの実験をして理論と整合をすれば、その系は完全に量子力学を満たす真の量子系であると断言できる強みがあります。
追記2:あるnoteで以下の批判がありました。ほぼ誤解だけの内容なのですが、コメントをこちらに書いておきます。
まず量子論に観測問題はないという主張は以下の理由で誤解だと主張されていました。
-
測定は『誰』が行えるのか?(例:無生物は測定できるのか?)
-
測定とは具体的にどのようなプロセスを行うことなのか?
-
測定は厳密にどのタイミングで行われるのか?(「波動関数はいつ収縮するのか?」のように表現される場合もあります)
これらの問題は,少なくとも完全な正解が得られていないという意味で未解決だという主張だそうです。しかしまず欠落している大きな視点として、これらは量子論固有の問題ではないことが指摘できます。確率を扱う理論で、初学者が混乱する部分を列挙しているだけのように思えます。例えば古典確率論において「測定は『誰』が行えるのか?」「測定とは具体的にどのようなプロセスを行うことなのか」「測定は厳密にどのタイミングで行われるのか?」という問題を挙げて、古典理論にも「観測問題」があると大げさに主張する方は、私は見たことがありません。量子論だけ特別扱いして「観測問題がある」と主張されるのが、むしろ不思議に思えます。また量子論でも古典論でも、挙げられた問題についての理解は既にあるわけです。ここで確率理論において「測定」とは以下のように定義しておきます。サイコロの目のように、ある確率分布をしている対象系の独立な事象(サイコロならば1から6の目が出る事象)からただ1つの事象(例えば3の目が出たという事象)が選ばれたという体験を「測定」と呼ぶことは自然です。少なくとも多くの方はサイコロの目は1から6のうちのどれか1つだけを観測認識していますよね?でも、確実に1つの事象が選ばれたと認識できたと主張できるのは、その人本人でしかありません。他の人間も同様に同じ目が出たと主張をしても、嘘をついている可能性すらあります。本当に1つの事象が選ばれたと言い切れるのは、飽くまでその<私>という意識をもったその人だけです。他の人間は実は意識を持たないAIであっても、実はその発言からは区別がつきません。ですからそもそも論として「測定は『誰』が行えるのか?」という問いは、実証科学的な答えを与えようがない不良設定問題なのです。形而上学的哲学としては問題に成り得ても、実証科学としては無意味なものなのです。
次に「測定とは具体的にどのようなプロセスを行うことなのか?」という質問ですが、これも量子論に限らない問題です。むしろ古典力学的領域の分野である脳生理学などの分野での問題とも言えます。これをもって「量子論には観測問題がある」と騒ぐのは、全くおかしなことだと思います。
「測定は厳密にどのタイミングで行われるのか?」という問いの大部分も、上の問題と同じで量子論固有の問題ではありません。また確率論において、測定を行う観測者の指定がなければ、「どのタイミング」も答えようがないのは自明です。観測者を指定すれば問題は設定可能です。その場合は、その観測者の脳に対象系の情報が記憶領域に格納されるタイミングこそが「測定」の時刻となるでしょう。これも脳生理学の問題となります。ですからこれによって「量子論に観測問題がある」と主張するのも、あまり内容がないと思えます。
また「測定を行うためには意識の存在が不可欠である」は誤解であるという主張がありました。これもおかしいです。測定とは多くの可能性の中からただ1つの事象が選ばれると認識することなのですから、その「認識」をする主体を前提として考えているはずです。その主体に便利のために名前を付けて「意識」としているだけの話です。本質的に中身のある内容ではありません。
次に「波動関数は実在しない」というのは誤解という主張もありました。実在の定義次第という理由らしいのですが、これもおかしいと思います。たとえば波動関数は現在では物理量の確率分布だけからきちんと数学的に定義される対象であることが明確になっています。前世紀のように正体不明な対象では無くなりました。波動関数の正体は単なる確率分布なので、波動関数を物理的実在だと呼ぶならば、確率分布も物理的実在と呼ばなくてはいけません。でも少なくとも数学的確率分布のことを物理的実在であると主張する人は極めてレアだと思います。確率分布はその対象系の事前知識の多寡によって観測者毎異なるからです。Aさんにとってのサイコロの目の確率と、Bさんにとっての同じサイコロの目の確率は、一般に異なってよいのです。(たとえばBさんは箱の中にあるサイコロの目を箱裏の窓からこっそり見て知っているけれど、それをAさんは知らない場合など。)つまり観測者の事前知識に対する依存性があるという理由で「確率は(物理的)実在でない」と自然に述べるのならば、「波動関数は(物理的)実在ではない」と明確に述べられるのです。
次に「この世界の全ては量子系である」というのは誤解だという主張についてです。私の立場では、これは「誤解」というよりも、様々な物理系に実験を行い続け、実証科学として検証し続ける研究テーマという位置づけです。一方で、これまでの多くの実験観測の結果からは、量子系ではないと判断された例は1つも見つかっておりません。その意味で「この世界の全ては量子系である」という仮定は、日々強化されている現状だと言えます。なお「量子系」の定義はこの補足で先に述べたものになります。ある未知の対象Xに対して、上に述べた方法で確実にXが「量子系」であるか否かを決定できます。一方で、専門家を名乗る人の中には、Xだけでなく宇宙全体を調べつくさないとXが量子系であるかどうか分からないという定義や主張をする方もいます。局所トモグラフィ性という性質が「量子系」であることを導くことに重要であると主張をされたりしていますが、宇宙全体を調べ尽くさないと、目の前にあるXが量子系であるかどうかを厳密に述べられない「量子系の定義」というものは、実証科学として全くの無意味だと思います。一方私の教科書では、ボルン則や量子重ね合わせを自然な条件から実際導いております。対象Xが上で述べた条件を実験で満たしていることが分かれば、自動的に導かれることだからです。
前世紀からの「量子論の観測問題」を無意味に延命させて、問題を混乱させるだけの主張をされる方もいるので、その著書を読まれる場合には、注意が必要かと思われます。
量子力学に「観測問題」は存在しない|Masahiro Hotta (note.com)

















 P114(7.44)式
P114(7.44)式

 P118 (8.10)式
P118 (8.10)式

 P136 下から10行目
P136 下から10行目

 追記(2022/7/1)
追記(2022/7/1)




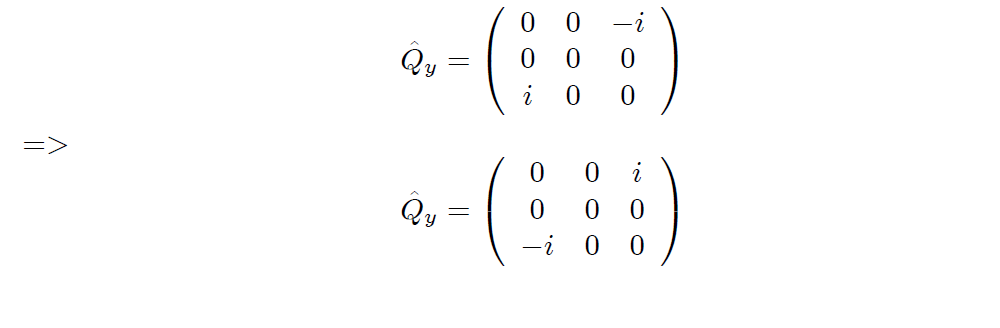
 追記(2022/12/3)
追記(2022/12/3) 追記(2022/12/9)
追記(2022/12/9)






























 このように認識論的な
このように認識論的な