量子エンタングルメントは、量子情報科学における量子テレポーテーションや量子コンピューティング用の資源として知られている。
今回は様々な物理学分野における精密測定の資源としても使える可能性がある、量子エンタングルメントの側面を紹介しておこう。
現時点でこの技術を使っているのは量子光学系の実験が主だが、これからは半導体を含む様々な物性系や素粒子・原子核系の実験、そして宇宙観測の技術にも入り込んでいく可能性もある。
物理学の多くの実験では、未知の相互作用プロセスの解明を目的にしている。
例えばヒッグス粒子の発見も、この粒子が関わる反応を精密に測定して達成されたものだ。
特に微小な結合定数等のパラメータの大きさの推定が重要な場合も多い。
そこで簡単な例を挙げて、パラメータ推定における量子エンタングルメントの有用性を説明したい。
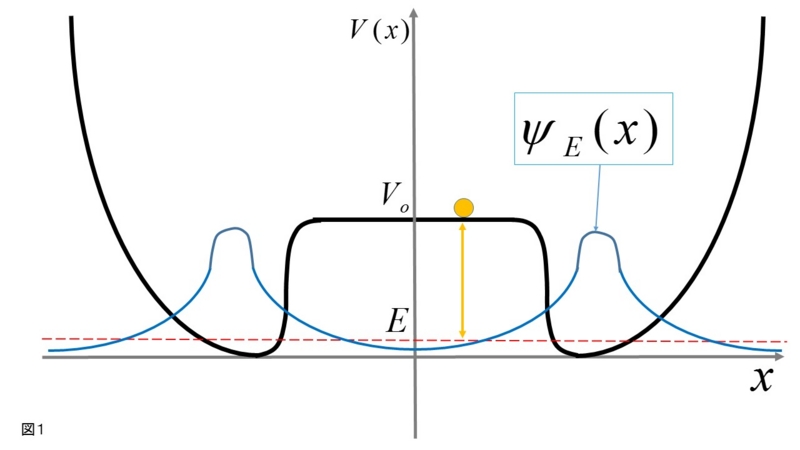
図１のような外から中が見えない箱がある。
中には、箱の正面と直交したある大きさの磁場がかけられている。
その箱にスピンがアップ状態にある電子を放り込むと、とても小さな角度θだけスピンは回転されるとしよう。
このθは未知であり、箱から出てきた電子のスピンを測ることで、θの大きさを推定したい。
そうすれば、箱の中の磁場の強さが推定できる。
従来の実験では図２のように、大量のＮ個の電子スピンを同じ状態に用意して、それぞれを箱に通してから個別に測定をして統計を溜める。
この場合、よく知られているようにθの推定誤差はNの平方根に反比例して減少する。
しかし量子エンタングルメントを用いると、Ｎ個の電子スピンを使ってもＮに反比例する推定誤差での推定が実現できるのだ。
これは従来の方法に比べて、Ｎの平方根分だけ、より精密なθの推定を達成している。
この高い精度のパラメータ推定を説明するために、図３のように箱を９０度回転させよう。
磁場の向きは、地面に垂直方向となる。
まず回した箱に電子のスピンアップ状態を放り込んで様子を見てみる。
するとスピンの向きは変わらないまま、箱から出てきてしまう。
ただ出てきたアップ状態は、入ったアップ状態に比べてθだけ回った位相因子exp(iθ)がかかっている。
もちろん状態ベクトル全体にかかる位相因子は物理量ではなく、どんな実験でも測れない。
だから図３の状況で出てきたスピンを測定しても全くθの情報を得ることはなく、図１の場合より悪化したように見える。
しかしθの推定精度を上げるヒントは、図４のようにＮ個のアップ状態を放り込んだ時に得られる。
出てくるＮ個のスピン系の状態には全体としてexp(iNθ)の位相因子が付いている。
小さなθの効果が、Ｎ倍になっている。
Ｎを十分に大きくすればNθは１程度にまでできるので、この増幅効果には期待が持てる。
しかし図４の場合でも、このNθは観測量ではない。
せっかくのＮ倍の増幅効果をいかすために、量子エンタングルメントを利用しよう。
図５のように、Ｎ個の電子スピンの量子エンタングルメント状態を考える。
Ｎ個全てのスピンがアップであるマクロ状態と、Ｎ個全てのスピンがダウンであるマクロ状態の足し算になっている。
これは（シュレーディンガーの）「猫状態（cat state）」とも呼ばれる。
このＮ個の電子を一個ずつ箱に通して上げると、最後にできる状態は図５の下の式のようになる。
Ｎ個全てがアップの状態の部分にはexp(iNθ)、ダウンの状態部分にはexp(-iNθ)の因子が付いている。
今度は２つのマクロ状態の間の相対位相因子としてexp(i2Nθ)が現れるが、これは観測可能量である。
そして２Ｎ倍の増幅効果のために、Δθ＝π/(2N)程度の誤差でθが推定できることが分かる。
従来の方法では(1/N)^(1/2)でしか減少しなかった推定誤差が、量子エンタングルメントのおかげで1/Nという速いスピードで減衰するのだ。
もちろんここでの議論には、デコヒーレンスの効果を抑えつつ、猫状態を制御できるという前提がある。
現時点では技術的に簡単には達成できない話だ。
しかし将来量子計算機の技術が進み、量子エンタングルメントの制御技術が上がるにつれて、このような量子パラメータ推定の現実味も増してくることだろう。
量子エンタングルメントを用いると、別なタイプの量子推定もできる。
図６のように２つのスピンＡとＢを考え、その量子エンタングルメント状態を用意する。
また未知の微小パラメータgに依存した操作をスピンに行う箱があり、Ａをそれに放り込む。
そしてＡにはgの情報が書き込まれる。
ここでAB両方を並べて二つを跨ぐ量子測定を行うと、量子エンタングルメントを使わない場合に比べて、gの推定誤差は一般には小さくなるのだ。
それはgの情報が単にＡのスピン本体に書きこまれるだけでなく、ＡとＢとの間の量子相関にgの情報が書きこまれる分も存在するからである。
ここでの議論の一般論は、量子フィッシャー情報量の理論を用いると厳密に構成できる。
量子フィッシャー情報量に関して、例えば[1]に解説がある。
また図６のような設定で、系から取り出せる情報が増えることを指摘した論文としては[2]が知られている。
また低ノイズ系での微小パラメータ推定の一般論は[3]にある。
[1]林正人, "量子情報理論入門", (SGC32, 別冊数理科学, サイエンス社）
[2]A. Fujiwara, Phys. Rev. A 63, 042304 (2001).
[3]M. Hotta, T. Karasawa, M. Ozawa, Phys. Rev. A 72, 052334 (11) (2005).
(追記：２０１６年日本物理学会誌１１月号「標準量子限界を超える高感度磁場センサに向けて」松崎雄一郎著（NTT物性科学研）の記事では、Nが１０の４乗のリンの電子スピン集団や、１０の７乗のダイヤモンドの電子集団での実装可能性が論じられている。日進月歩の技術進化が、どんどんと量子技術の境界を広げている。)
つまり考えている領域の外では、|Ψ〉でのいかなる物理量の期待値、分散、高次モーメント、そして揺らぎの相関が、無を意味する真空状態のものと区別がつかないということだ。
パルスをｙ軸の正の領域にあるスクリーンで捕らえれば、粒子がｘ軸上のどこの地点にいたのがパルスの横幅程度で分かる。
|ψ〉=c₊|+〉+c₋|-〉という量子状態に対して、アップとダウンの確率はそれぞれp₊=|c₊|²、p₋=|c₋|²であり、スピンｚ成分の値は確定していない。
